language : Japanese | English

ぼっち大好き

トップ貯蓄率とFIREまでの年数二次関数と虚数i 絵コピックメイキング曲絶対音感昔のソフトウェア Visual Studio C / C++ / MFC 備忘録日記作者

二次関数と虚数i

虚数iはどこにあるのか。

少々オカルトな話ですが、虚数iはどこにあるのかを説明するために、わたしの中にあるy=x²のグラフを絵にしてみました(2枚)。x,yの値を複素数に対応させるため、実空間RE(y)-RE(x)の他に、虚空間RE(y)-IM(x)、虚空間IM(y)-RE(x)、虚虚空間IM(y)-IM(x)と、その間の亜空間を含んでいます。これにより、解なしのx²+1=0が、交わっている個所を可視化できます。

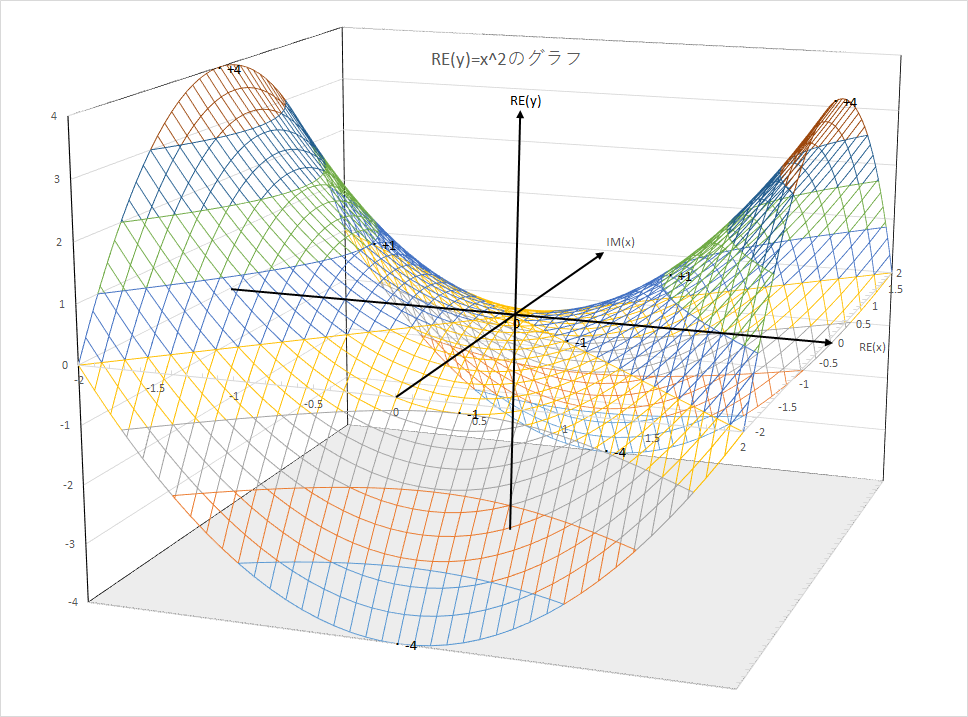
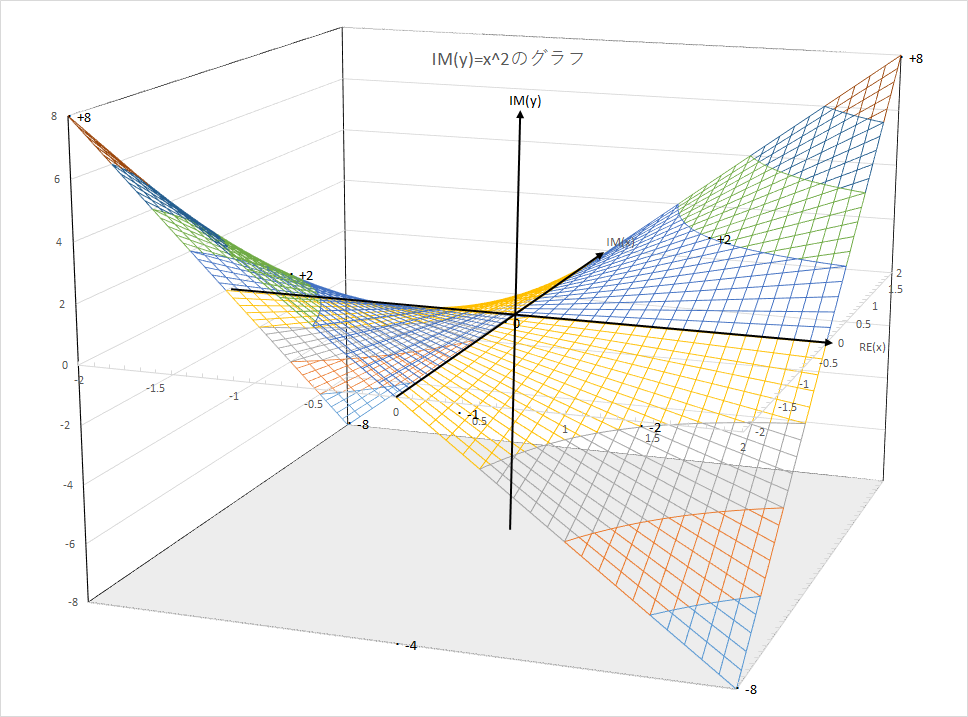
まず、x²=0の解ですが、RE(y)のグラフでy=0を満たすものは(0+0i)で交わる2本の直線上にあります。また、x²=0iも要求されているので、IM(y)のグラフでy=0を満たさなければならず、RE(x)=0とIM(x)=0の2本の直線上にあります。両者の共通部はx=0+0iのみ(単一解)となります。

次に、x²+1=0の解ですが、RE(y)のグラフを1だけ上にずらしてみると、y=0を満たすものはx=0±1iを含む2本の双曲線上にあります。また、x²+1=0iも要求されているので、IM(y)のグラフでy=0を満たさなければならず、RE(x)=0とIM(x)=0の2本の直線上にあります。両者の共通部はx=0±1iのみ(重解)となります。

なお、この変な形をしたグラフは、二次双曲面というらしいです。また、実部のグラフと虚部のグラフはy軸回りに45度回したのと同等です(多少伸縮がある点は異なる)。